✌️ Optimism and the Prisoner's Dilemma

A research report that was recently published stated what may sound obvious: optimism drives and enables coordinated cooperation.

And when you think about it, it's not weird at all, and the whole matter gets clearer when you look at it through a simplified model. If you are optimistic about other people's willingness to cooperate, it is more logical that you also cooperate. Mutual trust is created, which gets strengthened each time the expectation of cooperation is met.

This also explains why pessimists do not cooperate - if they do not believe that others will do it, why try even?

The power of being optimistic and thus expecting an equally optimistic response from others is essential for developing societies and civilizations. Another example that shows this is the Game Theory tournaments organized by Robert Axelrod.

The Prisoner's Dilemma

Axelrod was interested in how to best play the game called the Prisoners' Dilemma - a game in which you can choose to cooperate or defect from cooperation.

The game is simple: you have committed a crime together with a buddy. The police have taken you and your buddy and placed you in separate rooms. The prosecutor shows up and gives you both the same deal: if you snitch and
your partner stays silent, he gets 10 years in prison, and you go free (and you get 5 points). If you keep quiet and your buddy starts talking, you get 10 years in prison, and he goes free. If you both keep quiet, you get a maximum of 6 months in prison (and 3 points each). If you both tattletale, you both get 5 years in prison (or 1 point each).

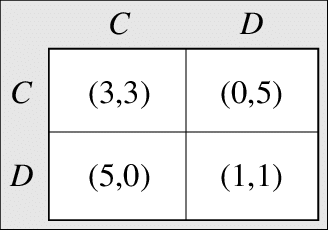
The most logical move here is not to stay silent and thus defect because it is also the most logical thing for the other person to do. So when you try to calculate what to do, you will conclude that you should snitch, ending with both of you getting 5 years in prison. In theory, you could have gotten away with only 6 months: hence the dilemma...

Axelrod was interested in how this game would develop if you played it over and over again. Then it suddenly becomes possible to remain silent. It is important in this context, however, to state that as long as the game is played a finite number of times that is given beforehand, it is not rational to do anything other than talking in the first round. But Axelrod created a tournament of the game where cooperation was possible because the game was won by getting, in total, as many points as possible.

So what does the best strategy look like in a game that continues over several rounds? Is it to be silent at random rounds? Or maybe trying to predict the likelihood of the other player defecting? Axelrod invited a number of different people to create strategies for his computer game tournament, where the strategies competed against each other in the Prisoner's Dilemma.

The winner was a program called Tit For Tat - this program started by collaborating and then did exactly what the opponent did in the previous round. But - and this is an important point - the program began by collaborating.

Tit For Tat was optimistic.

Had the program started on a position of defecting, while the opponent did the same thing, it would in all probability lead to a game with uninterrupted defecting—a vicious spiral of mistrust.

In extended studies, another computer program also succeeded well - "Tit For Two Tats" - a program that began by collaborating and then changed its behavior only after the opponent defected two rounds in a row. Tit For Two Tats was thus not only optimistic but also forgiving. An interesting lesson for the pessimist.

What does it mean in reality, then?

Even Tit For Two Tats can lose in cases where it plays against a program that deliberately takes advantage of forgiveness. So what is the lesson here? Is cooperation a kind of magic formula that always works? Maybe not, but cooperation is a kind of magical starting point.

When pushed to the limit- the alternative cost to always defect is high, when the alternative is to always be silent. It is possible to earn much more by being "kind" in a world of optimists. Although short-term thinking can pay off in one go, it risks ruining the entire future, as it does for pessimists.

In a realistic game, you do not know the number of rounds; you thus benefit from starting at a position of cooperation and a forgiving mindset. In wildlife and human interaction, the cost of creating a vicious circle of non-cooperation can be too great. There are also some studies that suggest that "Tit For Tat" is the "strategy" that governs the interaction of several animal species. Animals are also optimists!

Optimism that renews

But Tit For Two Tats teaches us something more. Forgiveness is also optimistic. Believing that someone will change and, for example, stop acting in a way that disappoints and hurts other people means that we believe that destructive patterns can end.

This belief has probably saved us many times.

Forgiveness is optimistic on two levels: it is based on optimism about our ability to change and our will to change.

Through this optimism, we can renew ourselves as human beings, and cooperation is completely dependent on us being able to come together once again after we have been divided as a group.

Without optimism, no civilization. So the next time you doubt cooperation and optimism, you can lean on having the research on your side.

Nicklas Berlind Lundblad and Elina Tyskling